Exercise 2-60(2)
What is the distance matrix represented by this graph?
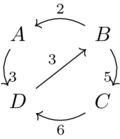
Solution(1)
| \(\rightarrow\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | 3 | 11 |
| B | 2 | 0 | 5 | 5 |
| C | 5 | 3 | 0 | 8 |
| D | 11 | 9 | 6 | 0 |
Can convert any weighted graph into a Lawvere metric space, where a the distance is the sum of weights along the shortest path.
It can be hard to see the shortest path by inspection, but a matrix power iteration method (starting from just a matrix of edge weights) is possible.
A metric space \((X,d)\)
A set \(X\) whose elements are called points
A function \(X \times X \xrightarrow{d} \mathbb{R}_{\geq 0}\) which gives the distance between two points.
These must satisfy three properties:
\(d(x,y)=0 \iff x=y\)
\(d(x,y)=d(y,x)\)
\(d(x,y)+d(y,z)\geq d(x,z)\) (triangle inequality)
An extended metric space includes \(\infty\) in the codomain of the cost function.
A Lawvere metric space
A Cost-category, i.e. a category enriched in the symmetric monoidal preorder \(\mathbf{Cost}=([0,\infty],\geq,0,+)\).
\(X\) is given as \(Ob(\mathcal{X})\)
\(d(x,y)\) is given as \(\mathcal{X}(x,y)\)
The axiomatic properties of a category enriched in Cost are:
\(0 \geq d(x,x)\)
\(d(x,y)+d(y,z) \geq d(x,z)\)
The set \(\mathbb{R}\) can be given a metric space structure, with \(d(x,y)=|x-y|\).
Imagine the points of a metric space are whole regions, like US, Spain, and Boston. Distance is "Given the worst case scenario, how far do you have to travel to get from region A to B?"
This actually breaks our symmetry requirement: \(d(Boston,US)=0, d(US,Boston) > 0\)
Which distance is bigger in this framework: \(d(Spain,US)\) or \(d(US,Spain)\)?
\(d(US,Spain)\) is bigger because there is much more room for the worst case scenario to place one farther for Spain.
A bigger first argument makes things strictly worse, all else equal. A bigger second argument makes things strictly better, all else equal.
Consider the symmetric monoidal preorder \((\mathbb{R},\geq,0,+)\) which is the same as Cost but does not include \(\infty\). How do you characterize the difference between this and a Lawvere metric space in the sense of definition 2.46?
It is a metric space in which points may only be finitely-far apart.
What is the distance matrix represented by this graph?

| \(\rightarrow\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | 3 | 11 |
| B | 2 | 0 | 5 | 5 |
| C | 5 | 3 | 0 | 8 |
| D | 11 | 9 | 6 | 0 |